深度学习-RNN

I. 前言

介绍RNN（Recurrent Neural Network）的概念和应用。

RNN是一种能够处理序列数据的神经网络，它在处理时考虑了之前的状态。因此，它可以对序列数据中的每个元素进行建模和预测。

RNN的应用非常广泛，尤其是在自然语言处理和时间序列分析等领域。以下是RNN在各个领域的应用：

1. 自然语言处理（NLP）

- **文本分类**：将文本归类到不同的类别中，如情感分析、垃圾邮件过滤、新闻分类等。

- **机器翻译**：将一种语言的文本翻译成另一种语言的文本。

- **语音识别**：将人类语音转化为文本。

- **文本生成**：根据给定的文本生成新的文本，如对话生成、诗歌生成等。

- **问答系统**：回答用户的自然语言问题。

2. 时间序列分析

- **时序预测**：根据过去的数据预测未来的数据，如股票价格预测、气温预测等。

- **行为识别**：根据传感器数据识别人的行为，如健身追踪、手势识别等。

- **异常检测**：识别与正常行为不同的行为或异常行为，如网络入侵检测、设备故障检测等。

除此之外，RNN还可以用于图像和视频处理等领域。

II. RNN基础

RNN的基本概念和结构：

1. RNN的概念和结构

- RNN是一种可以对序列数据进行建模的神经网络。

- 与传统神经网络相比，RNN增加了循环连接，使得网络可以处理序列数据中的时序信息。

- RNN的结构包含一个循环单元，可以看做是对于前一时刻的状态 \( ht−1 \) 和当前时刻的输入 \( x_t \) 的函数，即 \( ht=f(ht−1,xt) \)。

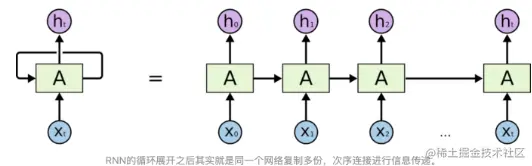
2. 详细结构示意图

- 下图是一个简单的RNN结构示意图：

```

x_t -> h_t -> y_t

```

其中：

- \( x_t \) 是当前时刻的输入。

- \( h_t \) 是当前时刻的状态，即循环单元的结果。

- \( y_t \) 是输出。

RNN如何工作？

1. 初始化状态：初始时，所有节点（包括隐藏层和输出层）初始化为零向量，此时网络处于空状态。

2. 输入更新状态：在每个时间步，输入 \( x_t \) 更新状态 \( h_{t-1} \) 通过激活函数 \( f \)。具体计算公式如下：

```

ht = f(ht−1, xt)

```

3. 输出产生结果：最终输出由当前状态 \( h_t \) 决定，可以看作是经过网络处理后的结果。

总结

RNN是一种强大的工具，它能够有效地对序列数据进行建模和预测，并在多个领域表现出色。

在每个时间步中，输入 \( xtx_txt​ \) 会与上一时刻的状态 \( ht−1h_{t-1}ht−1​ \) 经过一个带有权重矩阵 \( UUU \) 和 \( WW\) 的线性变换，然后通过激活函数 \( fff \) 得到当前时刻的状态 \( hth_tht​ \)。接下来，\( hth_tht​ \) 会作为下一时刻的输入状态 \( ht+1h_{t+1}ht+1​ \)，并与下一时刻的输入 \( xt+1x_{t+1}xt+1​ \) 经过相同的变换和激活函数，直到所有时刻的输入都处理完成。

最终，我们可以通过将所有时刻的状态 \( h_1,h_2,...,h_Th_1,h_2,...,h_Th_1,h2​,...,hT​ \) 经过一个带有权重矩阵 \( VVV \) 的线性变换，再通过激活函数得到每个时刻的输出 \( y_1,y_2,...,y_Ty_1,y_2,...,y_Ty_1,y2​,...,yT​ \)。输出的具体形式取决于具体的任务，如分类任务通常使用 Softmax 激活函数，而回归任务则使用线性激活函数。

RNN的前向传播和反向传播算法

RNN的前向传播和反向传播算法是神经网络训练的核心。在前向传播算法中，我们将输入序列逐步输入到网络中，并计算每个时刻的输出；在反向传播算法中，我们通过比较网络输出和真实标签之间的误差，计算每个参数对误差的贡献，并使用梯度下降算法来更新参数。

前向传播算法

假设我们的输入序列为 \( x_{1:T}=x_1,x_2,...,x_Tx_{1:T}={x_1,x_2,...,x_T}x1:T​=x1​,x2​,...,xT​ \)，其中 \( xtx_txt​ \) 表示第 \( ttt \) 个时刻的输入向量。我们使用 \( hth_tht​ \) 表示第 \( ttt \) 个时刻的隐藏状态向量，\( yty_tyt​ \) 表示第 \( ttt \) 个时刻的输出向量。

在前向传播算法中，我们首先将第一个时刻的输入向量 \( x_1x_1x1​ \) 与初始状态 \( h_0h_0h0​ \) 输入到网络中，通过一个线性变换和激活函数计算出第一个时刻的隐藏状态 \( h_1h_1h1​ \)，然后再将 \( h_1h_1h1​ \) 和第二个时刻的输入向量 \( x_2x_2x2​ \) 输入到网络中，依次计算出第二个时刻到第 \( TTT \) 个时刻的隐藏状态 \( h_2,h_3,...,h_Th_2,h_3,...,h_Th2​,h3​,...,hT​ \) 和输出向量 \( y_1,y_2,...,y_Ty_1,y_2,...,y_Ty1​,y2​,...,yT​ \)。具体的计算方式如下：

\( h_t=f(U_{xt}+Wh_{t-1}+b_h)t=h_t=f\left( U_{x_t} + W_{h_{t-1}} + b_h \right)ht​=f(Uxt​+Wht−1​+bh​)

\( y_t=g(V_{ht}+by)y_t=g\left( V_{h_t} + by \right)yt​=g(Vht​+by​)

其中，\( UUU \)、\( WWW \)、\( VVV \) 分别为输入、隐藏状态和输出的权重矩阵，\( bhb_hbh​ 和 \( byb_yby​ \) 分别为隐藏状态和输出的偏置向量，\( fff \) 和 \( ggg \) 分别为隐藏状态和输出的激活函数。

反向传播

首先，我们需要根据当前时刻的输出向量 \( yty_tyt​ \) 和真实标签 \( yt′y_t^\primeyt′​ \) 计算输出向量的梯度 \( \frac{\partial L}{\partial y_t}\frac{\partial L}{\partial y_t}∂yt​∂L​ \)，其中 \( LL\) 表示损失函数。具体来说，如果我们使用平方损失函数，那么输出向量的梯度可以表示为：

\( \frac{\partial L}{\partial y_t}=2(y_t-y_t^\prime)\frac{\partial L}{\partial y_t} = 2(y_t - y_t^\prime)∂yt​∂L​

接下来，我们需要利用反向传播算法依次计算每个时刻的隐藏状态向量 \( hth_tht​ \) 和输入向量 \( xtx_txt​ \) 的梯度 \( \frac{\partial L}{\partial h_t}\frac{\partial L}{\partial h_t}∂ht​∂L​ \)。具体来说，对于某个时刻 \( ttt \)，我们可以通过下面的公式计算隐藏状态向量 \( hth_tht​ \) 的梯度：

\( \frac{\partial L}{\partial h_t}=\frac{\partial L}{\partial y_t}\cdot W_{hy}^T+\frac{\partial L}{\partial h_{t+1}}\cdot W_{hh}^T∂ht​∂L​=∂yt​∂L​⋅Wyh​T​+∂ht+1​∂L​⋅Whh​T​

其中 \( WhyW_{hy}Why​ \) 和 \( WhhW_{hh}Whh​ \) 分别表示输出层到隐藏层和隐藏层到隐藏层的权重矩阵。

需要注意的是，在最后一个时刻 \( TTT \)，我们需要将 \( \frac{\partial L}{\partial hT+1}\frac{\partial L}{\partial h_{T+1}}∂ht+1​∂L​ \) 设置为零向量。

接着，我们可以利用隐藏状态向量的梯度 \( \frac{\partial L}{\partial ht}\frac{\partial L}{\partial ht}∂ht​∂L​ \) 计算输入向量 \( xtx_txt​ \) 的梯度 \( \frac{\partial L}{\partial xt}\frac{\partial L}{\partial xt}∂xt​∂L​ \)。具体来说，对于某个时刻 \( ttt \)，我们可以通过下面的公式计算输入向量 \( xtx_txt​ \) 的梯度：

\( \frac{\partial L}{\partial x_t}=\frac{\partial L}{\partial h_t}\cdot W_{xh}^T∂xt​∂L​=∂ht​∂L​⋅Wxh​T​

其中 \( W_{xh}W_{xh}Wxh​ \) 表示输入层到隐藏层的权重矩阵。

最后，我们可以利用输出向量的梯度 \( \frac{\partial L}{\partial y_t}\frac{\partial L}{\partial y_t}∂yt​∂L​ \)、隐藏状态向量的梯度 \( \frac{\partial L}{\partial ht}\frac{\partial L}{\partial h_t}∂ht​∂L​ \) 和输入向量的梯度 \( \frac{\partial L}{\partial xt}\frac{\partial L}{\partial x_t}∂xt​∂L​ \) 对模型参数进行更新。具体来说，我们可以采用梯度下降算法或者其他优化算法来更新权重矩阵和偏置向量，以便更好地训练模型。

需要注意的是，在实际应用中，我们可能需要对学习率进行动态调整，以便更好地训练模型。此外，在实现反向传播算法时，我们通常需要采用递归或者循环的方式进行计算，以便有效地利用历史信息。

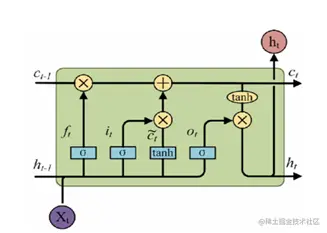
其中，圆圈表示神经元，箭头表示信息的传递。绿色方框表示输入门，红色方框表示遗忘门，黄色方框表示输出门。

LSTM的前向传播和反向传播算法与标准RNN类似，只是在计算中要加上门机制的计算。

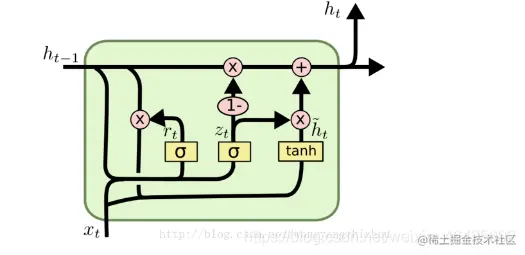
GRU

门控循环单元（GRU）是由Cho等人在2014年提出的。相比于LSTM，GRU更为简单，只包含了两个门机制：重置门和更新门。GRU的计算复杂度较低，训练速度也更快，而且在某些任务中性能表现与LSTM相当甚至更好。

GRU的结构如下图所示：

其中，绿色方框表示重置门，蓝色方框表示更新门。GRU的前向传播和反向传播算法也与标准RNN类似，只是在计算中要加上门机制的计算。

总的来说，LSTM和GRU都是为了解决标准RNN中的梯度消失或爆炸问题，并能够更好地捕捉序列中的长期依赖关系而提出的。两者的计算复杂度都比标准RNN高，在某些情况下，可能需要使用它们来替代RNN以提高模型性能。

在自然语言处理中的应用中，RNN可以用于文本分类、情感分析、机器翻译等任务。具体来说：

- 文本分类：将文本分为不同类别的任务

- 情感分析：判断一篇文章是正面的、负面的还是中性的

- 机器翻译：将一种语言的文本自动翻译成另一种语言的任务

时间序列分析中的应用包括时序预测、异常检测和行为识别。这些任务都需要处理长序列数据，RNN可以有效地捕捉并利用序列中的长期依赖关系。

进阶应用方面：

- 注意力机制和Seq2Seq模型是RNN在自然语言处理中应用的两个重要领域。

- 注意力机制可以让模型在处理长序列输入时，将注意力集中在与当前任务相关的部分，从而提高模型的性能。

- Seq2Seq模型是一种用于序列到序列转换任务的模型，如机器翻译和对话系统等。

多层RNN和双向RNN是另一种进阶应用。前者由多个RNN层堆叠而成，每个RNN层的输出都作为下一层RNN的输入；后者是由两个RNN组成的模型，分别是前向RNN和后向RNN，它们分别从输入序列的第一个元素开始以及最后一个元素开始处理。双向RNN能够更好地捕捉输入序列中的上下文信息。

结合RNN和CNN的应用，可以先使用CNN提取文本或图像的局部特征，再使用循环神经网络(RNN)对这些特征进行全局建模。这种结合方法可以帮助模型更有效地学习到时间和空间的信息，并提高模型的性能。

调参和优化是另一个重要的方面。学习率、正则化和丢弃等技术可以用于解决梯度消失和梯度爆炸等问题，而Adam、Adagrad和RMSprop等优化算法可以帮助我们更好地训练深度神经网络（DNN）模型。

最后，实践部分介绍了如何使用PyTorch实现一个简单的RNN模型，并演示了其在文本分类中的应用。通过实际操作，我们可以更深入地理解RNN的原理和应用场景。