《深度学习》李宏毅 -- task6卷积神经网络
在开始深入探讨卷积神经网络之前,我们先来讨论为什么需要使用卷积神经网络(Convolutional Neural Network,简称 CNN)。传统的深度学习模型通常包含多个层次的神经网络,每一层都试图捕获输入数据的不同特征。然而,在处理诸如图像这样的高维数据时,这种逐层抽象的方法往往无法有效利用图像中的局部结构和特征。
1. **局部感受野**:在卷积神经网络中,每一个卷积核(Kernel)都会以一个固定大小的窗口去扫描整个输入图像,并且仅对这个区域内有显著变化的部分进行响应。这使得CNN能够很好地捕捉到图像中的局部特征,比如边缘、纹理等。
2. **参数共享性**:通过使用多个卷积层和池化层,可以将不同位置的卷积核(Kernel)进行共享,在一定程度上减少了网络参数的数量,并且在训练过程中也大大提高了效率。
3. **特征级联**:CNN可以通过多层卷积来提取从局部到全局的不同层次的特征。比如第一层可能捕捉到图像中的一些边缘和轮廓,而更深层则能识别出更复杂的形状和结构,例如物体的分类特征。
4. **简化模型复杂度**:由于采用了池化操作(Pooling),CNN在网络构建过程中能够进一步减少参数的数量,这在处理大规模数据时尤其重要。此外,卷积层中的权重共享也减少了训练的难度和时间。
5. **效率高**:CNN架构设计使得它在计算资源有限的情况下也能有效处理图像数据,这对于嵌入式设备或移动应用来说非常有利。通过压缩计算量,提高了实际应用中的运行速度。
总的来说,卷积神经网络之所以能够广泛应用于图像识别、视频分析等场景中,是因为它们能有效地利用局部特征来捕捉和表示图像的复杂结构。
CNN常常被用于图像处理中,例如你需要对图片进行分类,这意味着你将训练一个神经网络,输入一张图片,然后将其表示为图片中的像素(像素)。输出则是(假设有1000个类别,则输出是一个长度为1000的向量)。
通常会遇到一些问题:
1.在训练神经网络时,我们希望在网络结构中每一个神经元都是一个最基本的分类器。事实上,在训练的过程中你可能会得出很多这样的结论。
2.直接使用全连接前馈网络进行图像处理时,需要很多参数。
CNN能简化神经网络的架构,并且在处理图像时,某些权重可以不使用,我们可以一开始就去掉这些权重。不是用全连接前馈网络,而是用较少的参数来进行图像处理。现在从以下三个方面进行阐述:
1.1 小区域(小区域)
这个方法的核心思想是将输入的图片表示为一个小区域内的像素值,然后对这些小区域进行特征提取和分类。这样可以减少训练时所需的参数,并且使得网络更易于理解。
2.2 窗口操作(Window Operation)
CNN在处理图像时使用窗口操作来提取局部特征。这种方法允许我们将输入的图片划分为多个小区域,每个小区域都可以作为一个独立的神经元来进行特征提取。这样可以减少所需的参数,并且使得网络更加简洁和易于理解。
3.3 模块化设计(Modular Design)
CNN采用模块化的设计来构建网络结构。这种方法允许我们将网络分解为多个子网络,每个子网络负责处理特定类型的图像特征。这样可以使网络更加灵活,并且可以根据需要进行调整和修改。
综上所述,CNN通过小区域的表示、窗口操作以及模块化的设计来简化神经网络的架构,减少训练时所需的参数,并使得网络更易于理解。
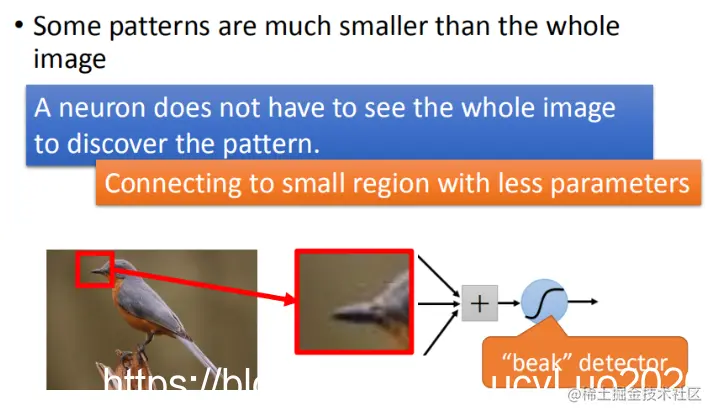
处理影像时,对于第一层的隐藏层,神经元的作用是侦测某一种模式,看它是否出现?大部分的模式其实比整个图片还要小。对一个神经元来说,假设它要知道图片中有没有某个特定模式,它不需要看整张图片,只需要查看图片的一小部分。
举例来说,假设我们现在有一张图片,第一个隐藏层中的某些神经元的任务就是侦测是否存在鸟嘴(有些神经元侦测爪子的存在,有些侦测翅膀的存在,有些侦测尾巴的存在,合起来就可以判断图片中是否存在一只鸟)。实际上它并不需要看整张图,只需要给神经元展示一小红色方框的区域(即鸟嘴),就能知道它是不是一个鸟嘴。对人类来说也一样,观察这一小块区域是否为鸟嘴,不需要查看整个图像就知道了。因此,每个神经元只连接到每一个小块的区域就可以了,不需要连接到整张完整的图。
1.2 相同的图案(Same Patterns)
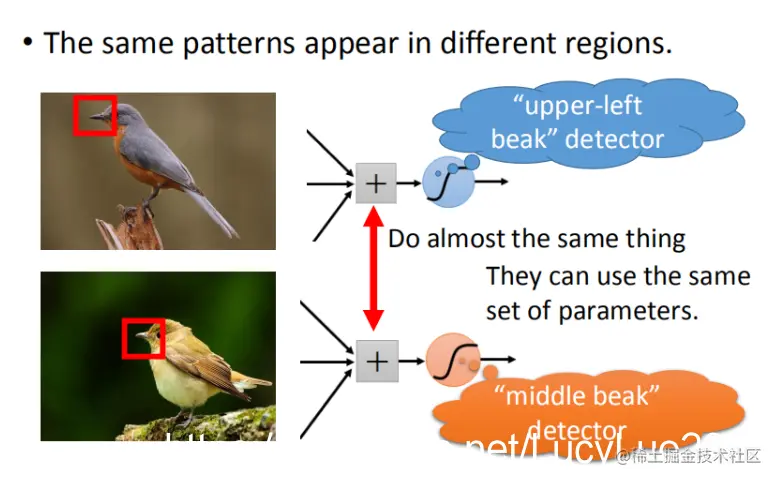
在观察上图时,相同模式在图像中可能出现在不同的位置,但它们代表的是同样的含义。这些图案具有相同的形状,并且可以通过相同的神经网络和参数来检测。
在这张图中,我们有一个位于左上角的鸟嘴,还有一个在中央的鸟嘴。虽然需要明确区分这两个鸟嘴的位置,但我们不需要为每个鸟嘴单独训练一个探测器(detector)。通过这种方法,我们可以避免冗余训练过程,从而减少所需的神经元数量。
例如,如果使用同一组参数来检测左上角和中央的鸟嘴,那么就可以减少参数的需求量。因此,我们并不需要为两个独立的任务分别设计不同的神经网络,只需用一个共同的参数集即可。
总结起来,通过这种方式可以大大简化系统的设计,从而提高效率并降低成本。
一个图像可以进行subsampling,即删除奇数行和偶数列像素,使得图像大小减半。这种操作不会显著改变人对图像的理解。通过这种方式,我们可以将图像缩小到原来的一十分之一大小。
三、卷积神经网络(CNN)架构
在使用CNN时,我们需要考虑如何选择合适的过滤器大小和步长。通常,较大的过滤器可以捕捉到更广泛的特征模式,而较小的过滤器则能更详细地处理局部细节。在实际应用中,我们常常会先尝试不同的参数组合,以找到最佳的卷积核尺寸和步长,这样有助于优化模型性能。
四、网络层的选择
为了构建一个有效的CNN架构,我们需要选择合适的网络层。常见的网络结构包括卷积层、池化层和全连接层。首先,我们会使用卷积层来提取图像中的特征;然后,通过池化层减少过滤器的数量,从而降低计算复杂度;最后,在全连接层中进行分类预测。
五、模型训练与优化
在训练CNN模型时,我们需要调整各种超参数以获得最佳的性能。这可能包括学习率、批量大小和网络结构等。使用交叉验证来评估模型的泛化能力,并根据结果选择合适的模型和参数。
六、数据增强
为了提高模型的鲁棒性和泛化能力,我们可以在训练过程中进行数据增强操作。例如,在图像数据集中添加随机旋转、翻转和缩放操作,这有助于训练过程中的多样性以及提高测试阶段的表现。
总之,构建一个有效的CNN架构需要综合考虑各种因素,并通过实验和调整来找到最佳的参数组合。
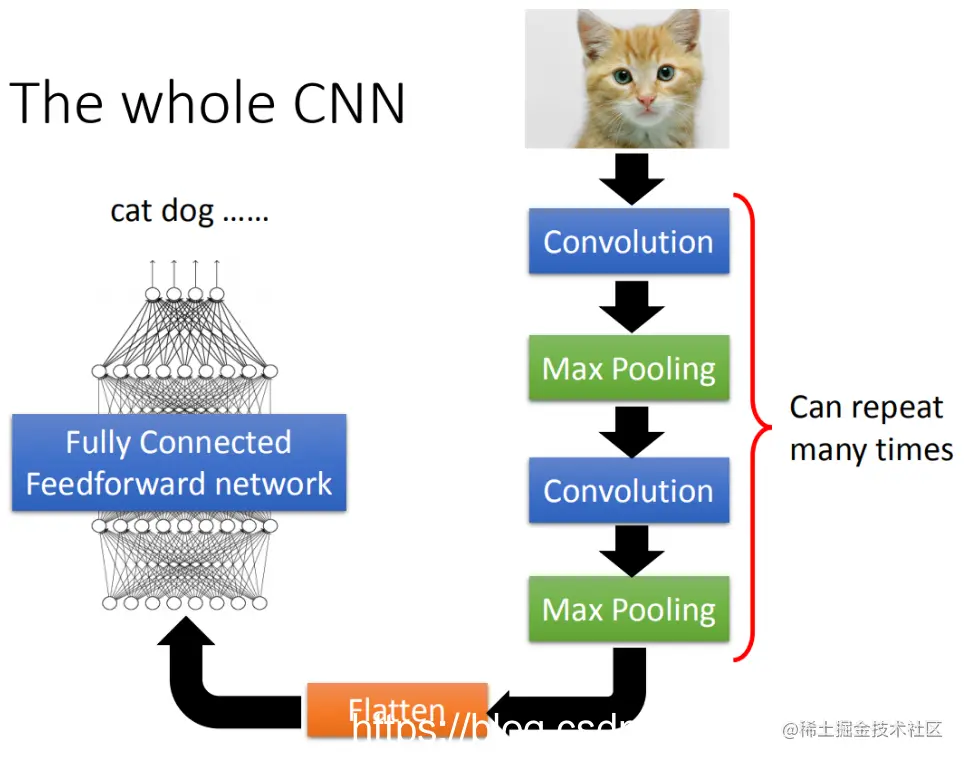
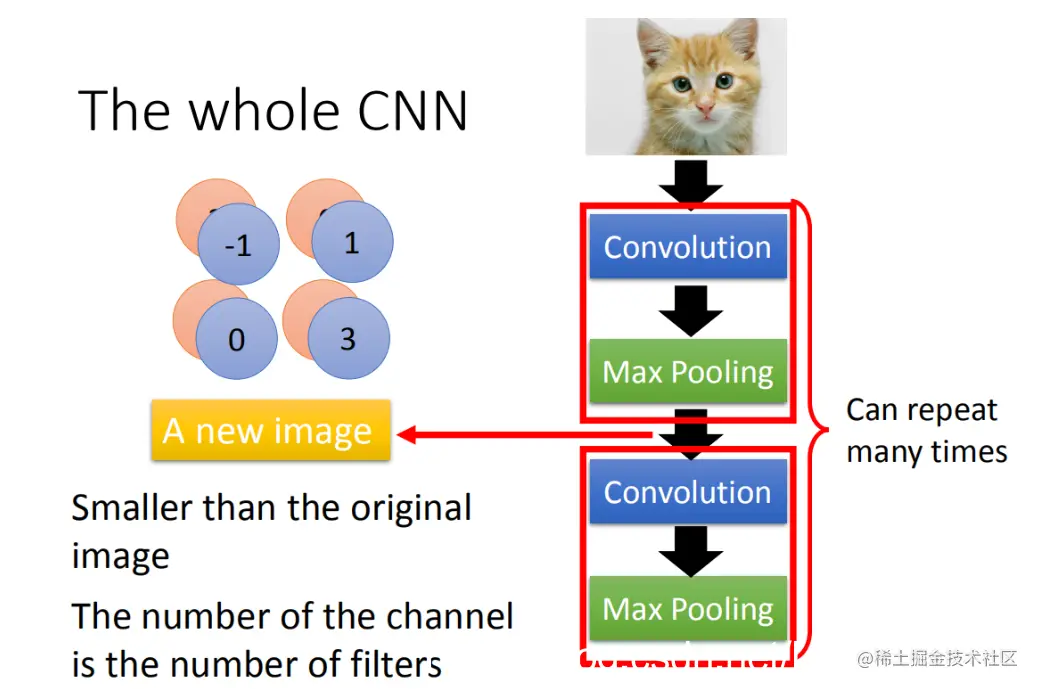
CNN的架构如下:
1. 输入一张图片后通过卷积层进行处理。
2. 然后进行最大池化操作(Max Pooling)。
3. 再次对输入图像应用卷积层(Convolution)。
4. 在这一步骤中,会重复上述过程多次;(具体重复多少次是事先决定的)
5. 最后将卷积后的输出丢入一个全连接前馈网络(Full-Connected Feedforward Network),从而得到影像辨识的结果。
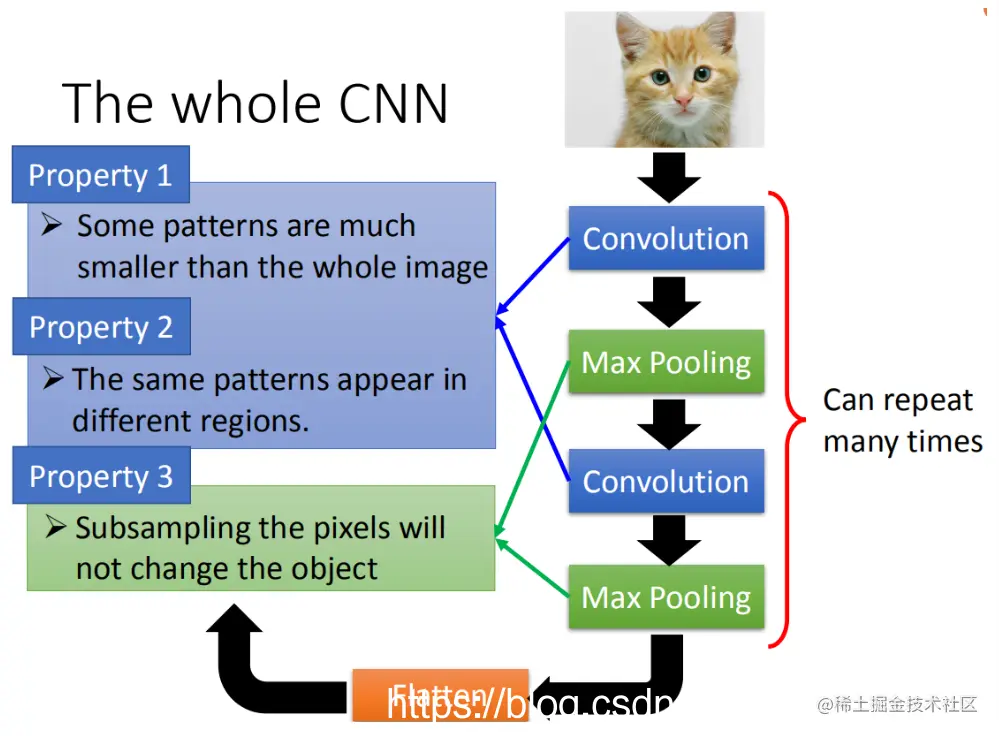
基于前面三个影像处理的结果观察:
第一,生成一个pattern,不要看整张图像,只关注图像的一个小部分。
第二,通用的pattern会在一张图片的不同区域出现。
第三,可以采用subsampling。
前两个特性可以用convolution来消除,最后一个特性则可以通过Max Pooling来处理。
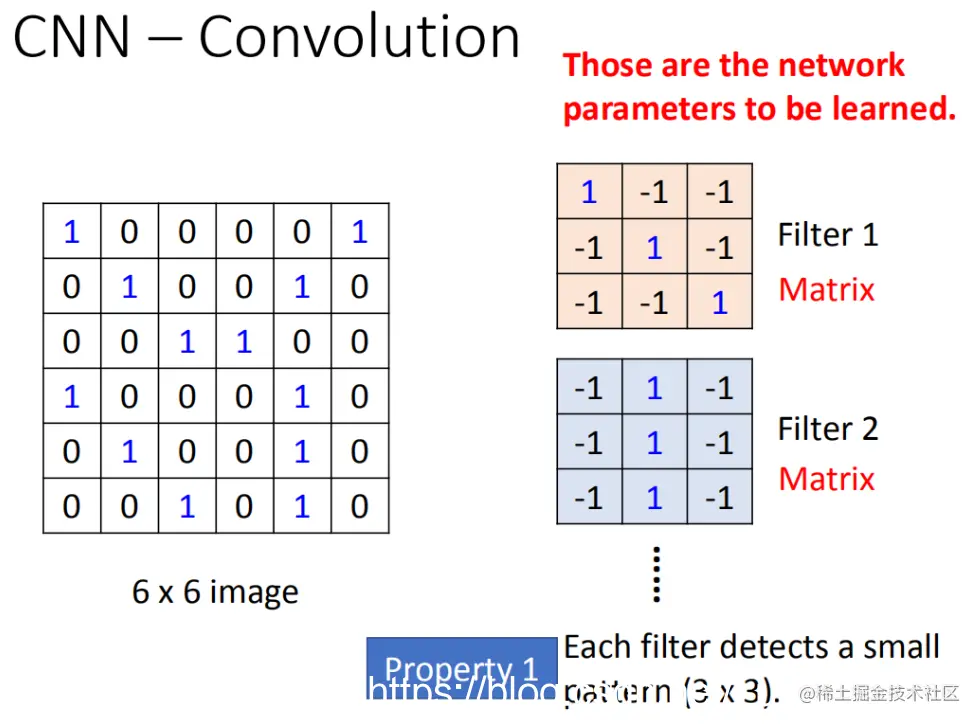
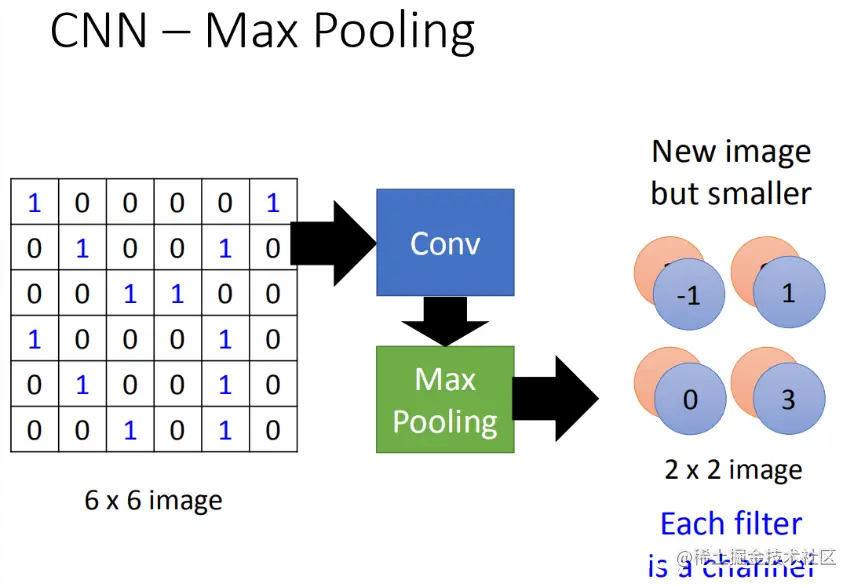
假设现在网络的输入是一个6x6的黑白图像。
对于这样一个6x6的灰度图,如果它只包含黑白两色,则每个像素只需要用一个值来描述它们的状态。例如,1代表有墨水,0则代表没有墨水。因此在卷积层中,我们有一个过滤器组(filter group),其中每一个过滤器实际上就是一个3x3的矩阵——matrix (3 x 3)。
这个矩阵内的每个元素都是网络参数的一部分,这些参数需要学习而不能事先设计好。
每个过滤器检测一个3x3范围内的模式。当卷积层使用过滤器时,并不是对整个图像进行遍历,而是只在每一个过滤器的3x3范围内寻找模式。
这就是我们考虑的第一个属性:侦测模式的能力。
接下来:
3.2 属性2(Propetry2)
...
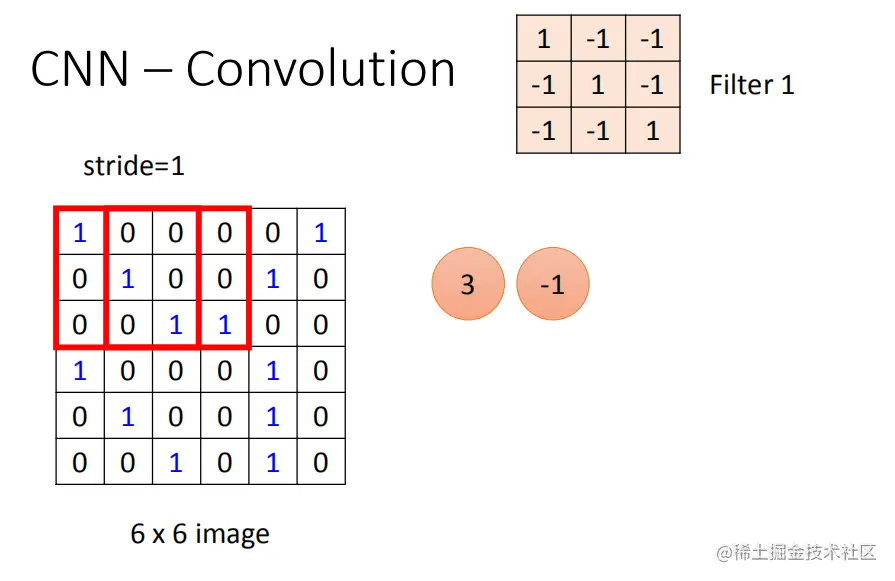
filter和image如何运作?
首先,有一个3*3的矩阵filter,把它放在image的左上角。然后,我们将filter的9个值与image的对应区域内的9个值进行点乘(内积),斜对角线上的值取1. 内积的结果将给出结果通道的数量。这个移动距离叫做步长(stride),你可以自己设计。
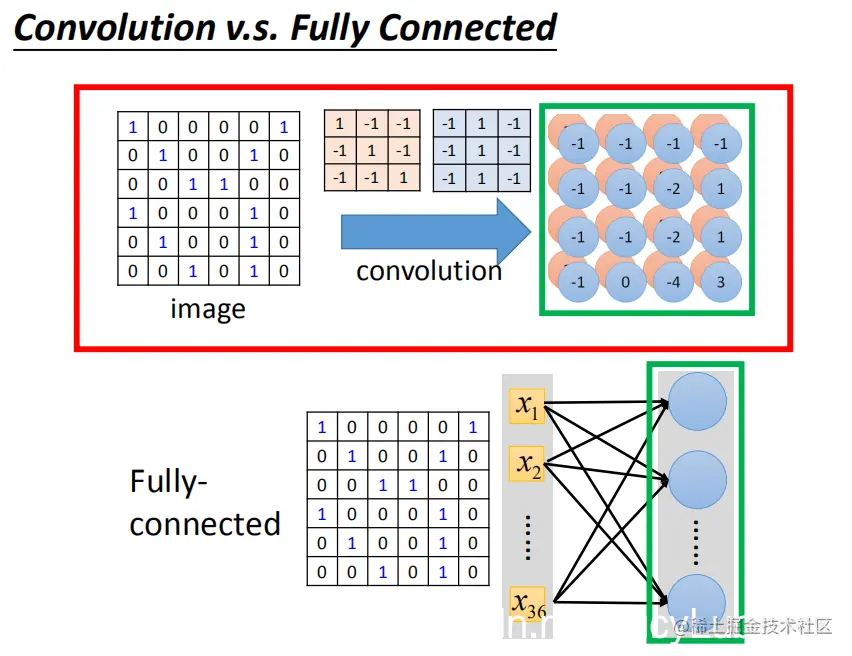
接下来,我们来谈卷积和全连接之间的关系。
全连接通常用于构建神经网络的输出层或分类器中的最后一层,通过全连接层可以实现多输入到单输出的功能。
另一方面,卷积是一种特殊类型的全连接。它在深度学习中非常常见,特别是在图像识别任务中。卷积层通过应用滤波器(一个固定大小的矩阵)来提取特征,而不是直接处理整个输入数据。
### convolution与全连接层的关系
**convolution** 是一种完全连接层,它将某些权重去掉。经过卷积后的输出实际上是一个隐藏层神经元的输出。
如果将这两个链接在一起的话,卷积就是完全连接拿掉一些权重的结果。
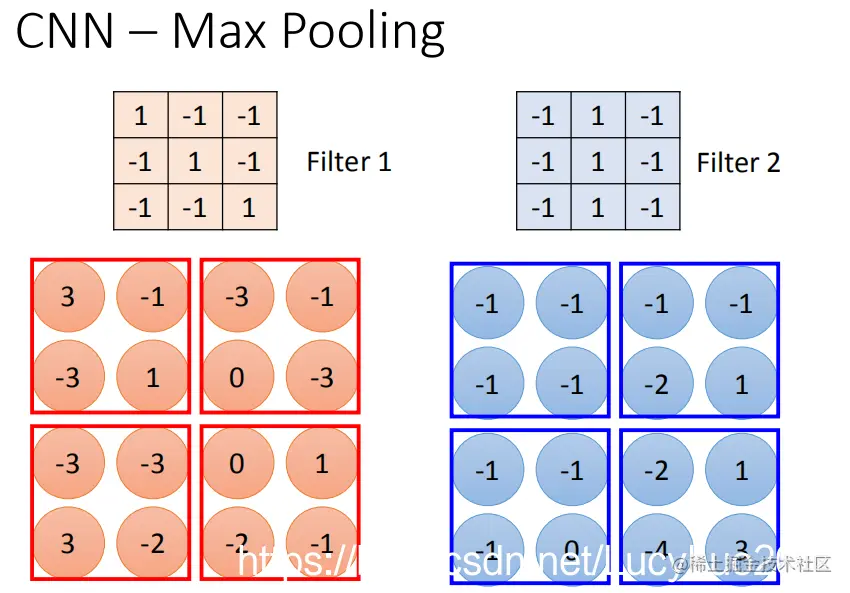
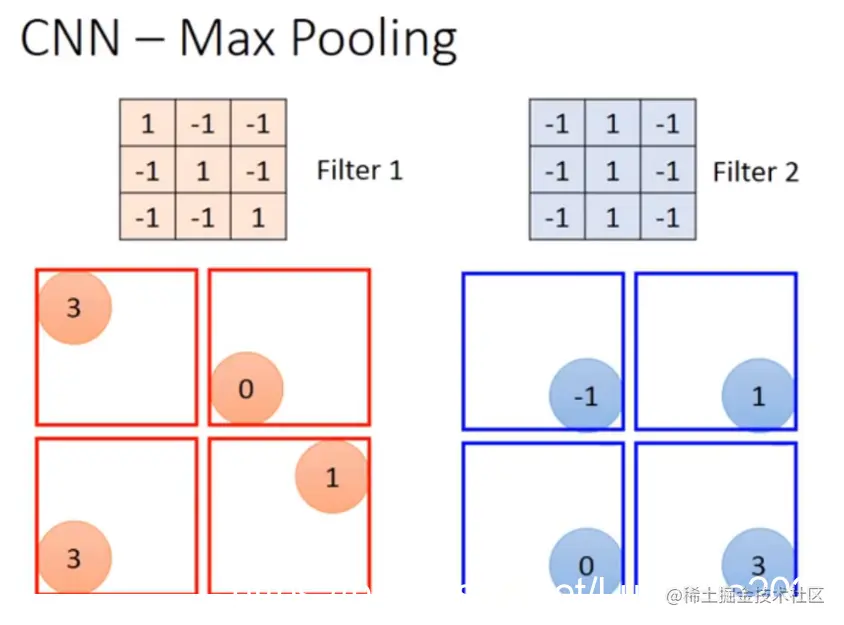
### Max pooling的操作原理
Max pooling是一种减少输入特征图尺寸的方法,用于简化模型。它的核心思想是通过选择每个区域中的最大值来表示该区域。在二维空间中,它会将一个二维数组(即特征图)分割成若干小块,并从每一块中选出最大的一个数字作为该块的输出。这样做的目的是为了减少数据量并降低计算复杂度。
### Max pooling的具体操作步骤
1. **分组**: 将输入特征图分成多个小区域,通常是固定尺寸。
2. **提取最大值**: 对每个小区域内所有元素进行比较,并选择最大的一个作为该区域的输出。
3. **填充**: 为了保持输入和输出的形状一致,可能会在边界处填充一些零(或使用某种方式替换这些零)。
Max pooling通过这种方式大大减少了特征图的维度,从而简化了模型结构。这不仅有助于提高训练速度,还能减少过拟合的风险。
在原始图像中应用两个不同的滤波器以生成一个新的4x4的矩阵。首先使用filter 1获取第一张图像中的四个像素值,并将其与第二张图像中的对应像素值相比较,计算出它们的最大值或平均值。然后将这些值组合成一个新值,形成一个包含四个元素的新矩阵。最后,通过这个新的矩阵来缩放原始图像。
假设我们从四组数据中挑选出最大值,这可能带来一个问题:当我们把这些值存储在一个神经元中时,无法使用微分法来对它进行计算。不过,我们可以采用另一种方法来解决这个问题。
在卷积神经网络(CNN)中,进行一次卷积操作后,输入图像的维度会有所变化。以6 x 6像素的图像为例,在执行了卷积和最大池化之后,它会被压缩成一个2 x 2的特征图。
卷积操作会生成新的通道数,每个通道对应于一种不同的滤波器(kernel)。每个滤波器都对输入图像的一个特定区域进行处理。这个区域的大小取决于我们选择的滤波器尺寸,通常滤波器是3 x 3或5 x 5等,以减少噪声并提取更清晰的信息。
在执行卷积操作后,像素的数量会从原来的6 x 6变为2 x 2。新生成的特征图将包含多个通道,每个通道对应于一个不同的滤波器。
在处理图像数据时,我们可以使用卷积层和最大池化层来实现多次卷积操作。每个卷积层输出的特征图尺寸会逐渐缩小,最终生成一张小尺寸的图片。
例如,第一次使用25个过滤器,得到25个特征图,然后对这25个特征图再次进行卷积操作,每次都会得到一个更小的图像。
然而,这个过程并不仅仅通过一次25个过滤器来实现。实际上,第二次处理时会考虑输入图像的深度信息,并不是单独对待每个通道。因此,即使第一次使用了25个过滤器,输出特征图的数量仍然是25个(即滤波器数量)。
假设第一次有2个过滤器,第二次也有2个过滤器,则其最终卷积操作得到的特征图数应是 2 * 2 = 4 个。然而,这并不意味着最终结果会是 25 * 25^2 的特征图,因为每个过滤器都是一个立方体。
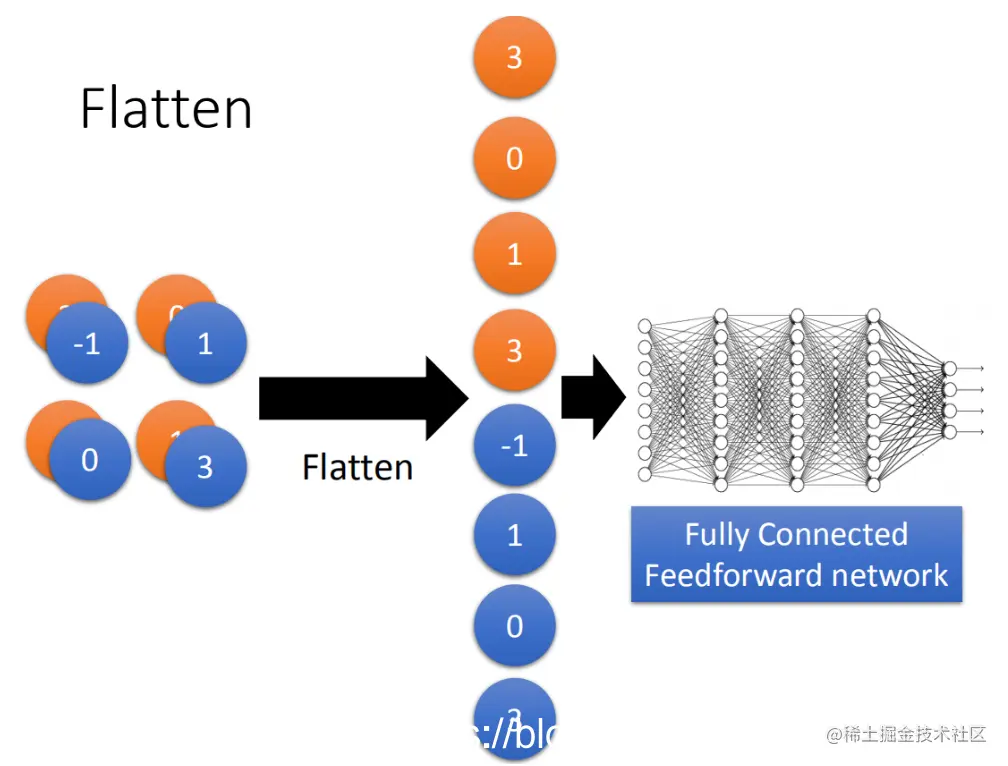
七、压平(Flatten)
接下来,我们需要将这些卷积层输出的特征图进行压平处理。压平层的作用是从高维空间转换到低维空间,以便于后续网络层处理。
特征图(feature map)是一种图像数据的表示形式。在卷积神经网络中,输入的数据通常是多通道的彩色图像。为了便于后续处理,我们需要将这些图像转换为一维向量或者线性空间。这一过程称为特征图拉直。
具体来说,在卷积神经网络的第一步——卷积层,会使用多个滤波器(或称核)从图像中提取特征。每个滤波器对图像的每一个像素进行处理,并产生一个输出值,即特征映射(feature map)。这些特征映射构成了我们原始图像的多通道表示。
为了将这个多通道数据压缩为一维向量,我们需要设计一些机制来捕捉不同位置上的特征之间的关系。例如,在深度学习中常用的池化层就是一个很好的选择,它可以对特征图进行降维处理,保留每个区域内的最大值、平均值或某种统计特性,从而得到一个更紧凑的表示。
接着是全连接(fully connected)网络的部分。在特征图被拉直后,我们可以将其输入到一个卷积神经网络中的全连接层中,这些层通过线性变换将特征映射转换为分类或回归的目标空间。最后,利用softmax函数或者其他激活函数进行输出的归一化处理。
因此,特征图拉直是深度学习中一个重要步骤,它使得模型能够更容易地从高维数据中提取有用的特征,并且可以进一步进行全连接网络的学习和训练。